قانون مساحة المستطيل بالرموز مع ذكر مثال
المستطيل هو أحد الأشكال الهندسية الذي يتميز بكونه منتظم الشكل ويتكون من أربع أضلاع، فيه كل ضلعين متقابلين متساوين في الطول، والزاوية بين كل ضلعين تكون قائمة، قانون مساحة المستطيل بالرموز من أكثر الأسئلة شيوعًا حول هذا التعريف، ومن خلال هذا المقال سوف نتحدث عن إجابته بشيء من التفصيل.
قانون مساحة المستطيل بالرموز مع ذكر مثال
من خلال السطور التالية سوف نتحدث عن قانون مساحة المستطيل بشيء من التفصيل، والتي تتمثل في الآتي:
- مساحة المستطيل تساوي حاصل ضرب الضلعين كالآتي: مساحة المستطيل = الطول * العرض، وهنا يمكن معرفة مساحته بمعلومية أبعاده.
- يمكن معرفة مساحة المستطيل بمعلومية محيطة وأحد أبعاده من خلال هذا القانون، مساحة المستطيل = (المحيط× العرض – 2× مربع الطول) /2.
- مساحة المستطيل = (المحيط * العرض- 2× مربع العرض) /2.
- يمكن معرفة مساحة المستطيل بمعلومية قطره وأحد أبعاده من خلال هذا القانون، مساحة المستطيل = الطول× (مربع القطر- مربع الطول) ^ (1/2).
- مساحة المستطيل = العرض× (مربع القطر- مربع العرض) ^(1/2).
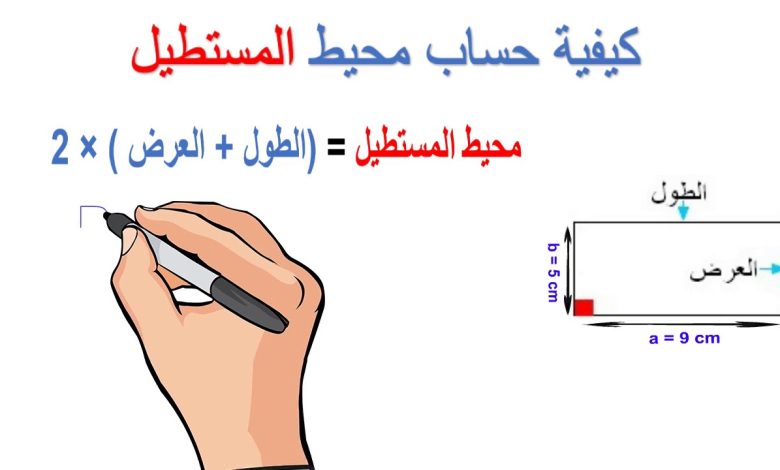
قانون محيط المستطيل
من خلال القوانين التي نعرضها لكم عبر السطور التالية يمكن حساب محيط المستطيل بسهولة، تلك القوانين تتمثل في الآتي:
- يمكن حاسب المحيط بمعلومية مساحته وأحد أضلاعه مستخدمًا هذا القانون: (2× المساحة+ 2 × مربع الطول) / الطول.
- يمكن حساب المحيط بمعلومية طوله وعرضه مستعينًا بهذا القانون: 2× الطول الأول(الطول) + طول العرض الثاني(العرض).
- يمكن حساب المحيط بمعلومية قطره وطول أحد أبعاده، مستخدمًا هذا القانون: 2× (الطول+ مربع القطر- مربع الطول) ^ (1/2)).
أمثلة على حساب مساحة المستطيل ومحيطه
من خلال السطور التالية سوف نقدم لكم أمثلة مختلفة عن حساب مساحة المستطيل ومحيطه والتي تتمثل في الآتي:
- أوجد مساحة المستطيل الذي طوله 2 سم وعرضه 3 سم؟
- الحل: مساحة المستطيل = الطول × العرض.
- المساحة = 2×3=6 سم2.
- أوجد مساحة المستطيل الذي محيطه 6 سم وطوله 2 سم؟
- مساحة المستطيل= (المحيط× الطول- 2× مربع الطول) /2.
- مساحة المستطيل= (6 ×2-2×4) /2=4سم2.
خصائص المستطيل
من خلال السطور التالية سوف نتحدث عن الخصائص التي يتميز بها المستطيل، وتلك الخصائص تتمثل في الآتي:
- جميع زوايا المستطيع تكون قائمة بتساوي 90 درجة.
- يحتوي المستطيل على بعدين ألا وهم الطول والعرض.
- مجموع زوايا المستطيل تساوي 360 درجة.
- فيه كل ضلعين متقابلين متوازيين.
- يعتبر المربع شكل من أشكال المستطيل لكن يختلف عنه في تساوي جميع أضلاعه.
- مربع القطر يساوي مجموع مربع طول الضلعين حسب نظرية فيثاغورث.
- كل قطر من أقطار المستطيل ينصفه إلى مثلثين متطابقين.
- المستطيل له نفس خواص متوازي الأضلاع.
- المستطيل له محوري تماثل ومركز تماثل واحد فقط.
- جميع أقطار المستطيل متساوية بحيث ينصفا بعضهما لبعض.
في الختام وصلنا لنهاية المقال الذي شرحنا فيه أحد الأشكال الهندسية المميزة ألا وهو المستطيل، كما وضحنا القوانين المناسبة لحساب مساحته ومحيطه مع ذكر بعض الأمثلة البسيطة وكذلك تحدثنا عن خصائص المستطيل التي تميزه عن الأشكال الهندسية الأخرى في عالم الرياضيات.